MATEMÁTICAS Y CORONAVIRUS: ¡QUÉDATE EN CASA!

      El Coronavirus acaba de saltar de una especie animal al hombre, razón por la que nadie tiene anticuerpos para combatirlo, lo que se traduce en que toda persona infectada desarrolla una carga viral y se convierte en nuevo foco de infección. Por eso la elevada capacidad infecciosa. No pasa lo mismo con la gripe, para la que hay una masa de personas que ya la han pasado y que aunque alguien resulte infectado no se convierte  en nuevo foco.

   La velocidad de expansión del virus depende de varios factores pero se mide por el llamado valor R0, que es el número promedio de personas infectadas por otra ya infectada y el tiempo medio que tarda una persona en poder contagiar a otra.

    Para el coronavirus el R0 inicial es en torno a 2,7, un valor alto, y el tiempo promedio es de 5-7 días.  Esto significa que cada 6 días el número de infectados se multiplica por 3. Esto es 1, 3, 9, 27, 81, 243, 729, 2187, 5461, 19.683…. En menos de dos meses. La gráfica resultante se denomina en matemáticas una curva exponencial. Por eso es muy importante reducir el valor R0 para contener la rapidez de la expansión.

 

 

  Podemos predecir qué va a ocurrir siguiendo el modelo SIR, dónde S son “susceptibles” (toda la población en nuestro caso), I son “infectados” (con o sin síntomas, pero que son foco de infección) y R son “recuperados” (personas curadas o que han superado la enfermedad y que dejan de ser foco de infección, al no desarrollar desde ese momento carga viral suficiente para infectar).

    Dado que los síntomas son leves, el objetivo debe ser evitar que la curva crezca muy rápido a fin de no colapsar el sistema sanitario. Esto es, que el paso de I a R sea lento, porque si es rápido no habrá suficientes medios para todos y muchas personas que podrían salvarse morirán por falta de atención adecuada.

  Y esto implica cambiar R0. Si R0>1, entonces la pandemia progresa, pero si R0<1, entonces la pandemia se asfixia y termina por desaparecer. Esto no significa que el virus muera, significa que ganamos tiempo para  atender ahora o mas adelante a los enfermos con mas medios o incluso armas específicas, evitando muertes.

   Los factores que afectan a R0 son las características propias del virus, las condiciones medioambientales (temperatura y humedad) y la probabilidad del contagio debido a la densidad de personas y a su comportamiento higiénico.

  Sobre el primero no podemos actuar. Sobre el segundo, es de esperar que el virus se comporte como los demás virus respiratorios y se alcance el pico máximo en primavera y desaparezca en verano. Pero esto es una suposición, no una certeza. No podemos esperar que la diosa Fortuna trabaje para nosotros.

     Así que resulta imprescindible actuar sobre los otros factores: higiene y evitar el contacto entre personas. Dado que la curva es una exponencial, la tardanza en tomar esta medidas se traduce en un número enorme de contagiados… y muertos claro.

     Además hay que tener en cuenta que el número de casos confirmados es muy inferior a los contagiados, ya que muchas personas pasan la enfermedad sin síntomas y necesitan de 15 a 25 días para pasar de I a R. Días que están contagiando. Algunos autores indican que puede ser una relación 9:1 infectados:casos positivos. En esencia, el valor real de I es muy superior a los casos positivos de coronavirus, que son los que nos dan en las gráficas. Por eso la más mínima sospecha de una curva exponencial en base a casos positivos, es seguridad de que ya la curva es exponencial en valores de I.

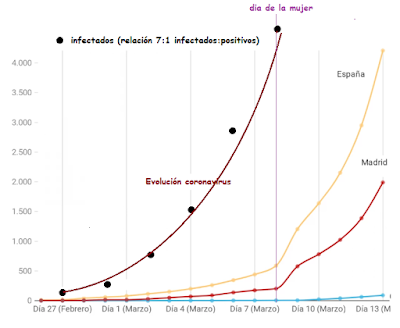
    El que la curva parezca muy plana al principio no debe confundirnos: sigue siendo una exponencial, es un efecto debido a la escala (cuanto mas alto el final de la curva, mas plana nos parece al principio). Pero es que si representamos los valores de infectados en una relación modesta 7:1 infectados:positivos, nos aparece en toda su claridad la curva exponencial.

 

 

   La conclusión es que el da 4 de marzo ya teníamos certeza de que la curva era una exponencial y que el virus no estaba controlado. En esa fecha ya se debería haber tomado decisiones para disminuir R0. Que el gobierno alentara las manifestaciones del día de la mujer fue una gravísima irresponsabilidad, ya que aceleró la propagación del virus, aumentado el valor de R0, por concentración masiva de personas. Y hoy la comunidad de Madrid lo está pagando en número de vidas.

    Pero además se tomaron decisiones que condujeron a diseminar el virus por toda España (éxodo de madrileños hacia las playas). Dos días antes les decía a mis alumnos que deberíamos hacer como Italia y que veríamos el ejército en las calles. Hoy se ha cumplido la profecía con la UME desplegada en grandes ciudades.

    ¿Y qué podemos esperar?. Los expertos dicen que no se pueden hacer cálculos precisos. Correcto pero como poder, podemos hacerlos. Hagámoslos.

    En los últimos 8 días y, tomando como referencia el dia de la mujer (ese día que “no pasaba nada para no celebrarla”), el ritmo de positivos es el doble cada dos días (589, 1639, 3004, 6252 en el día de ayer). Este es un ritmo muy elevado, que además fue propiciado por las manifestaciones. Supongamos un ritmo mas bajo: duplicación cada tres días. El ritmo de positivos será de 12.000 para el martes (dia 17), 24.000 para el viernes (día 20), 48.000 para el lunes y  96.000 para el jueves dia 26.

     Esa es la estimación para el comienzo del aplanamiento (en China tardaron esas dos semanas y media).  Ojo, positivos declarados, porque si no hacemos test, habrá positivos que no cuenten en ese valor.

  Estos datos se estiman si seguimos el actual ritmo de crecimiento. Si somos benignos y suponemos que empezarán a crecer al ritmo de Italia (duplicar el número de positivos cada cuatro días) la estimación será de unos 37.000 casos positivos.

     Al final (siguiendo el ejemplo de China) podemos terminar en torno a los  70.000 casos.

     En Sevilla, a un ritmo de duplicar cada 3 dias, estaremos en unos 900 casos con el control de la pandemia.

     Creo que son cifras lo suficientemente altas como para seguir las instrucciones:

 

                                      QUÉDATE EN CASA

¡FRÍO ABSOLUTO!

     Muchas veces me sorprende el desconocimiento que muestran alumnos de procesos o conceptos científicos que llevan estudiando de forma repetida a lo largo de muchos años. El asombro pinta en sus rostros cuando consigo que visualicen el azaroso viaje del oxígeno desde el aire hasta sus células ( y el viaje de vuelta del CO₂) y el objetivo que este proceso cumple en nosotros.

Y todo ello a pesar de tener  la costumbre de respirar continuamente.

    Otros de estos conceptos son los de calor y temperatura. Les sorprende que las palabras “frio” o caliente” sean algo relativo: si introducimos una mano en agua a 40 ºC  decimos que está fría si la otra mano se introduce en agua a 60 ºC, pero decimos que está caliente si el otro recipiente contiene agua a 20 ºC.

    Se extrañan cuando afirmo que el frio no existe. Sólo existe el calor. Claro que me refiero al calor como magnitud física, no como sensación. Todos ellos han observado que al poner un cuerpo caliente en contacto con otro frío, empieza a pasar energía del caliente al frío, hasta que se igualan las temperaturas. Esa “energía en tránsito” es lo que los físicos llaman calor.

    La temperatura, sin embargo, es una medida de la cantidad de energía que contiene un cuerpo y que puede ser “sacada” en forma de calor. Es decir, mide de alguna manera la cantidad de energía térmica que contiene un cuerpo. Cuando un cuerpo cede energía térmica a otro, observamos que ser transfiere calor. Los objetos tienen energía térmica pero no tienen “calor” (ni mucho menos “frio”).

    ¿Confundidos?. No se preocupen es normal estarlo. Son conceptos tan  esquivos, que a los científicos les costó mucho entenderlos o medirlos con precisión. Pensemos en la temperatura.

    Los primeros intentos para fabricar un termómetro datan del siglo XVI pero no fue hasta un siglo después cuando Farenheit y Celsius (en 1742) fabricaron termómetros con una precisión aceptable y  con una escala asociada. Para ello  se necesitaba una propiedad que variase de forma proporcional a la temperatura, a fin de relacionar ambas.

    Se basaron en el aumento de volumen del mercurio con la temperatura. Se introduce mercurio en un bulbo unido a un tubo muy fino (un capilar). Al aumentar la temperatura el mercurio se dilata y sube por el capilar.

   Para fabricar el termómetro asignamos de forma arbitraria (a nuestra elección) dos valores de temperatura a dos situaciones en las que sepamos que la temperatura se mantiene constante. Celsius eligió 0 ºC (Farenheit 32) para la temperatura de fusión del agua (cuando coexisten agua en estado líquido y sólido y la temperatura es fija)  y 100 ºC (212 ºF) para la de ebullición. Si dividimos en 100 partes iguales la zona de capilar entre los dos puntos a los que ha llegado el mercurio tenemos la escala centígrada.

   Sin embargo este tipo de escalas no esa aceptable en física porque la temperatura medida depende de la naturaleza de la sustancia usada (los valores medidos por un termómetro de mercurio y uno de alcohol son diferentes). Además no hay una proporcionalidad entre la temperatura y la energía térmica contenida en la sustancia.

     Estos inconvenientes fueron subsanados por William Thompson (lord Kelvin) en 1848. Su escala de temperatura es absoluta: no depende de la naturaleza de la sustancia y la temperatura es proporcional a la energía térmica contenida en ella y se relaciona con  la velocidad con la que se mueven los átomos y moléculas que forman los cuerpos.

     ¿Existen límites en los valores que puede alcanzar la temperatura?. Resulta que no lo hay  para la temperatura máxima que un objeto puede alcanzar pero si para su valor inferior y es 0 K. Este valor se conoce como cero absoluto de temperatura y es inalcanzable. No se trata de que no tengamos la tecnología para ello, es que es imposible que un cuerpo llegue a tener dicho valor. ¿Por qué?.

     La Física clásica tiene al menos tres respuestas para ello:

     Respuesta 1: según la Física clásica la materia está formada por átomos y moléculas en continuo movimiento al azar. En los gases las moléculas se  mueven con casi total  libertad mientras que en los líquidos se mueven menos libremente  pero permaneciendo juntas. Si bajamos mas la temperatura las moléculas se quedan en posiciones fijas, vibrando,  y tenemos un sólido. Pero a 0 K las partículas estarían quietas, lo que va en contra de nuestra descripción de cómo es la materia, lo que es absurdo.

    Respuesta 2: Se sabe (Ley de Charles) que el volumen de un gas es directamente proporcional a su temperatura si mantenemos constante su presión. Si medimos ambos valores se obtiene la gráfica de la figura. Prolongando la gráfica hacia atrás encontramos que a – 273’15 ºC (0 K) el volumen del gas es cero. ¡Pero un gas real cualquiera no puede tener volumen cero, ya que sus moléculas ocupan espacio!. Por lo tanto 0 K es imposible de alcanzar.

    Respuesta 3: Una máquina térmica es aquella que hace un trabajo extrayendo calor de un foco caliente y enviando calor a un foco frío ( La máquina de vapor es una máquina térmica, en la que la caldera es el foco caliente, la atmósfera el foco frío y el movimiento del tren es el trabajo realizado). El trabajo realizado es la diferencia entre ambos calores (de acuerdo al principio de conservación de la energía).

   La eficiencia ( E ) de nuestra máquina es el trabajo realizado entre la energía consumida  E = W/Qc.  La máxima eficiencia se consigue cuando toda la energía consumida se convierte en trabajo y vale 1 (ya que W = Qc).

   Además E = W/Qc = (Qc - Qf) / Qc = 1 – Qf/Qc. 
  Pero la definición de temperatura nos garantiza que (y aquí deben creer que no les engaño) podemos escribir que Qf/Qc = Tf/Tc. Si esto es verdad, la máxima eficiencia se conseguirá cuando el cociente Tf/Tc valga cero. Para conseguirlo tenemos dos opciones: o usamos un foco caliente a temperatura infinita (absurdo) o un foco frío a 0 K. 
    Se puede decir entonces que  una máquina térmica de máxima eficacia se corresponde a una temperatura de 0 K en el foco frío pero… ¡no pueden existir máquinas térmicas de eficiencia máxima!.  Es imposible transformar toda la energía consumida en trabajo, ya que el rozamiento entre las partes que componen la máquina y entre ésta y el medio disipan parte de la energía consumida en forma de calor. Lo que nos lleva otra vez a concluir que 0 K es un límite inalcanzable.

  Así que  según a Física clásica 0 K es inalcanzable. ¿Qué dirá la nueva Física nacida de la revolución científica del siglo XX?.

   La base de la Física moderna es la dualidad onda-corpúsculo, lo que significa que los átomos y las partículas elementales (electrones, protones) se pueden comportar como partículas o como ondas (nunca las dos cosas a la vez) según el experimento que el observador le proponga. No se trata de dos comportamientos diferentes, sino de una naturaleza única que puede presentarse como dos aspectos muy distintos.

  Otro principio básico es el conocido como el principio de incertidumbre de Heisenberg, que nos dice que no podemos conocer con exactitud y a la vez la posición y velocidad de las partículas . Aunque muchos filósofos han querido interpretar esto como una mera limitación a la precisión con la que podemos realizar las medidas, el principio de Heisenberg es parte de la naturaleza mas íntima de la realidad y subyace en la misma esencia de la dualidad antes comentada.

  Ambos principios llevan a decir a la nueva Física que el cero absoluto no se puede alcanzar: si lo pudiéramos hacer las partículas estarían quietas (recuerden que 0 K significa velocidad cero de las partículas que componen la sustancia). Unas partículas  quietas significa violar ambos principios: sabríamos con exactitud y la vez dónde está la partícula y con qué velocidad (0) y además excluiríamos la posibilidad del comportamiento ondulatorio de la partícula, ya que una onda está deslocalizada en el espacio (igual que una ola ocupa parte de la superficie del estanque).

   ¿Lo tienen claro?.

    Pues ahora les vuelvo a confundir: una temperatura kelvin negativa es posible de imaginar para los físicos, que la interpretan como que el sistema está más “caliente” que otro con temperatura positiva  ( y mas caliente que el cero absoluto).

  ¿Cómo que “mas caliente”?. Pues sí, un objeto con temperatura negativa absoluta cede calor a uno con temperatura positiva, luego está mas caliente.

  No, no piensen que están locos: ya se ha conseguido "calentar” cien  mil átomos de potasio a unas milésimas de kelvin por debajo del cero absoluto.

LA LARGA MARCHA

    Sábado por la mañana. Desayuno viendo un refrito del programa “Got Talent”. Un repartidor hipster de cerveza de mil kilos  intentar comer mas de ochenta flanes en minuto y medio. Sólo consigue comer setenta y dos, mancharse la barba de flan y provocarse arcadas a si mismo, a Risto Mejide y ,casi, a mi.  Después, un anciano de setenta y muchos años al que tiembla el micrófono (no por nervios) canta una especie de rap bajuno, dedicado a un amigo al que han abandonado:

                          “Que te como el pepe,

                            que te lo voy a comer,

                            con jamón de pata negra,

                            y un poquito de paté”

       Vuelven las arcadas al jurado (había que ver la cara de Edurne). A mí se me atragantan los churros. Lamentable.

   Por último una chica danza un baile clásico al ¿ritmo? de una música horrorosa. Sorprendentemente pasa al siguiente nivel, lo cual demuestra el poco “talent” del programa y del jurado. Hombre, no todo el mundo puede bailar eso, pero de ahí a “tener talento” va un mundo, cuando hay cientos de chicas como ella.

   ¿Qué es lo que nos pasa para que haya personas que se crean que pueden llegar a ser  héroes cuando hacen cosas estúpidas?.   ¿Por qué el talento sólo se busca en lo inútil o que reporta poco a mejorar nuestra vida?.  

   Pienso en los antihéroes, aquellos  que nunca aparecerán en ”got talent”:  alumnos que se matan en el bachillerato para ser médicos, arquitectos, físicos. Tengo que escribir algo para ellos.

    Entonces me acuerdo de Stephen King,  un maestro de novelas de terror,  muchas de las cuales han sido la base para guiones de grandes películas. Lo que poca gente sabe es que también escribe novelas,  y muy buenas, de ciencia-ficción y fantasía (como “los ojos del Dragón”). Una de ellas me recuerda mucho a la etapa por la que pasan los alumnos del bachillerato.

   La novela se llama “La larga Marcha”. En un país del futuro la sociedad lleva una vida altamente vigilada por un sistema político muy autoritario. Las únicas vías de escape son “juegos” salvajes, ofrecidos a todo el pueblo por televisión las 24 horas. Uno de los mas seguidos es “la Larga Marcha”.

  El juego consiste en andar por una carretera muy larga (tipo la ruta 66 en Estados Unidos) a un ritmo determinado. Si bajas del ritmo te dan un aviso para que aceleres. Si vuelves a bajar el ritmo, te dan un segundo aviso y al tercero te disparan  y mueres. No hay meta y sólo hay un ganador, qué es el único que sobrevive. En el sitio exacto de cada muerte se levanta un mojón para aumentar la tensión sobre los participantes  . Por supuesto, el ganador es un héroe y la cantidad de dinero que obtiene es astronómica.

   La novela se centra en el juego pero también, como tema transversal, describe el ambiente agobiante, el tipo de sociedad carente de libertad que lo soporta. Por ejemplo uno de los participantes es el hijo del presidente-dictador, que lo hace harto del autoritarismo de su padre.            

           El bachillerato es, salvando las distancias, como una larga marcha de dos años. Con el objetivo de llegar mas lejos que otros alumnos, tan lejos como la nota de corte de la facultad elegida. No vale con “andar”, por aprobar. Hay que seguir el ritmo de los mejores, si es que quieres entrar en la facultad que deseas. Esto último es especialmente cierto en facultades de ciencias, como medicina o el doble grado de matemáticas y física.

     En la novela hay mojones en la línea de salida, a  los pocos pasos de ella o muy lejos de ella, pero demasiado cerca de la meta. Igual pasa el en bachillerato: hay alumnos que ni siquiera vienen a clase y hay otros que se ve desde el momento cero que no van a dar muchos pasos y dejarán los estudios muy pronto.

    También hay corredores que no saben a qué están jugando y se dan cuenta, demasiado tarde ya, de que no aguantarán el ritmo infernal y que van a morir pronto. En el bachillerato hay alumnos que  no hacen nada para cambiar el ritmo. Siguen al paso de tortuga de secundaria, pensando que ya vendrán tiempos mejores, esperando el milagro de que el profe te apruebe. Por supuesto puede ocurrir que aprueben…. o puede que pongan un mojón con su nombre cerca de la meta.

    Pero no nos pongamos trágicos: El bachillerato es una maratón, no una carrera a muerte en un cuento de ciencia-ficción…… siempre  y cuando no quieras hacer medicina o biotecnología, claro. Pero es una maratón: o comprendemos la importancia del esfuerzo diario permanente o no llegaremos a la meta.

   Por eso es tan importante para el alumno comprender en profundidad en qué consiste el juego. Y además hacerlo cuanto antes mejor. Por eso, y siguiendo el consejo de mi antigua alumna María, que acabó el curso pasado, animo a mis alumnos de bachillerato a leer el último post que escribí en junio del año pasado.

    Sin embargo, donde encontramos mas diferencia entre la novela y la realidad de los estudios del bachillerato y de algunas de las carreras profesionales que hay detrás, es el resultado final para los ganadores.

   En la novela eres un héroe, multimillonario y apreciado por toda la masa social. En la realidad, la sociedad aprecia poco el tremendo esfuerzo que hay que hacer para llegar a la meta, y más si es una profesión de servicio público, como médico o profesor.

   Es triste comprobar cómo los grandes héroes de hoy son aquellos que, como en el libro de Stepehn King,  sobresalen en el ocio: deportistas (Nadal, Messi, Marc Márquez, Joaquin), artistas (Madonna, Julia Roberts) o incluso modelos de  pasarela. Pero no se valora el esfuerzo para ganar de personas que mejoran nuestra vida o la cambian. Personas que nos salvan la vida (literalmente) pero que nunca serán héroes para la masa social. Sólo servidores.

SUPERPROFESORES

           Leo una entrevista en “El Mundo” a David Calle, el profesor de la academia “Unicoos” que optó a mejor profesor del mundo. Le llaman “El superprofesor” y ahora da clases en la universidad sobre motivación de  alumnos. La innovación educativa de David descansa en dos ideas: ser un “youtuber” de la educación (subir “videos” explicando algún concepto de asignaturas de ciencias) y tener un grupo de “wasa” con sus alumnos.

                ¿Es David un buen profesor?. Sin duda lo es. Yo he visto sus vídeos y sus explicaciones son claras y sencillas. Y el estar en contacto constante con sus alumnos les ayuda mucho seguro.

                Es posible que dentro de poco escuchemos ( y aquí hago de pitoniso) hablar de otro superprofesor de ciencias. Se trata de Pablo Osorio que rige la Academia Osorio. Su twitter “Química Pau” está de moda y sus libros parecen ser la piedra filosofal que permite obtener unas notas fantásticas en Química de bachillerato y PAU. Llevo meses siguiéndolo y he estado varias veces a punto de comprar su libro “Una química para todos”.

                Ayer cayó en mis manos la pieza y era exactamente lo que yo pensaba que iba a ser. La idea innovadora de Pablo es reducir hasta el máximo lo que los alumnos deben saber y comprender para obtener buenas notas en la PAU y en la asignatura de Química de segundo de bachillerato. Un ejemplo: el tema de átomos  que se trabaja en un mes (16 h de clase), en su libro se reduce a unas ocho páginas, de las cuales 4 son ejemplos guiados y una es una tabla con muy poco texto.

                La idea del libro es muy buena para una academia (es exactamente lo que yo haría si mi objetivo fuese el que mis alumnos de academia obtengan buenas notas). Pero es eso: un paradigma de resultadismo en la educación, aunque también consigue que los alumnos aprendan y se motiven. Sin duda Pablo es un buen profesor.

                ¿Puedo ser yo un superprofesor?. Para serlo topo con una dificultad enorme: no me muevo en el mismo medio ambiente que Pablo y David. El mero hecho de ir a una academia ya supone una gran ventaja:  hay una  selección natural de los alumnos. Yo me muevo en un medio mas salvaje, dónde encontramos especies de alumnos de todos los tipos en su hábitat natural. Mis objetivos son diferentes: debo enseñarlos a pensar por sí mismos, a que aprendan mucha química pero también que amen la ciencia, que escriban mejor, animarles a que lean, a que se pregunten cosas, a que sean mejores personas, mas adultos, mas responsables. Y todo en un ambiente que puede no ser bueno o incluso malo o muy malo.

                Así que debo intentar de todo. Arriesgar en mis clases (a veces mas de lo que me gustaría sin duda), inventar (y hacerles participar en) pequeñas payasadas y “performances” para demostrar visualmente una idea científica; realizar sencillos experimentos que les rompen los esquemas de lo que hace un profesor, contarles historias paralelas a la ciencia que estudian. Siempre pensando que el fin (que me escuchen, no que me “oigan”) justifica los medios.

Intentos por buscar ese equilibrio imposible entre máxima exigencia en sus conocimientos científicos y adecuar los resultados a sus esfuerzos y a las expectativas que esta sociedad cada vez mas resultadista y menos formativa espera de ellos.

Piensen que  durante  años de primaria y secundaria los acostumbramos a que los problemas los resuelvan otros. A pasar de curso sean cuales sean los resultados, a regalarles títulos que significan poco o nada, a sufrir clases  destrozadas por alumnos “disruptivos” cuyo supuesto derecho a estudiar, que nunca ejercitan, siempre esté por encima del suyo; a exigirles lo mínimo para que otros no se queden atrás.

Y, de repente, se encuentran con bachillerato. Dos cursos en los que no sólo se les exige que tengan la responsabilidad que antes no les hemos dado, sino que además deben competir con todos los otros alumnos del mundo para entrar donde ellos sueñan. Miles de exámenes, millones de nombres y conceptos duros, a veces incomprensibles incluso para mí (lo siento profesor Santi, pero hay filósofos cuyo pensamiento es mas enrevesado que el nudo gordiano de Alejandro Magno). Deben luchar con todo ello y mas: las manías de cada profe (ése que si no pones “solución:” te quita puntos (yo mismo), aquel que te deja la asignatura para el examen final porque tienes alergia a los vectores; el otro que no te pone sobresaliente porque no has justificado los márgenes o escribes “hotel” en vez de “posada” al comentar el quijote), la inseguridad de enfrentarse a la espada de Damocles de la PAU e incluso tener que escribir sin cometer ninguna falta de ortografía.

Por eso mis alumnos de segundo de bachillerato son mi guía para saber si puedo “aspirar” a superprofe. Esos chicos que hoy se van y empezarán muy pronto la aventura universitaria. A algunos de ellos los conozco desde hace cinco años, cuando eran unos críos que levantaban sólo, es un decir, medio palmo del suelo. Imberbes ellos, niñas ellas.

El cómo me hablan y lo que me dicen es lo que me vale.

Me valen esas pequeñas charlas con Pepe, José , Daniel (aunque no esté este año en mis clases) y Juan Jesús en el recreo. Comprobar como Pepe se acuerda (¡después de cinco años!) de que no se puede probar una patente de una máquina que produzca mas energía de la que consume, es un orgullo para mí.

Me sirve oir como María Jesús dice que soy yo el que le enseñó química y, claro está, como se curra su 10 en química. Como Pepe (otro Pepe) comenta que mis guiones son mejores que el libro “una química para todos”; aunque no me fio mucho porque me halaga en exceso ( y eso que ya le dije, tiempo ha, que de chico me vacunaron contra los halagos y soy inflexible en mis notas).

Hoy incluso alguno dice que nunca me olvidará. Ya veremos. Pero sólo el hecho de decirlo ya justifica mi dedicación, mi trabajo. Deben madurar tanto en tan poco tiempo, que resulta increíble que sobrevivan sin volverse locos. Y, aún así, algunos dicen que se acordarán siempre de alguno de nosotros, en vez de querer largarse y olvidarnos.

Esto es lo único que nos hace a los profes seguir adelante: venir a clase afónicos, quedar en el recreo para cantar en el coro o dar clases gratis de inglés para preparar el “Trinity”.

Alguien echará de menos que no hable de sus notas. No es un olvido: sus notas son su éxito. El mío es que tengan claro que sus notas son el fruto de su esfuerzo y de mi trabajo. No soy un superprofesor, pero tampoco lo necesito: el trabajo diario y callado, invisible la mayoría de las veces, es lo verdaderamente importante para aquellos que están a nuestro cargo.

                No quiero acabar el post sin unas últimas palabras para ellos: confiad siempre en vosotros mismos como yo lo he hecho siempre. Y si alguna vez se os olvida esto o alguien os  dice lo contrario, no dudéis en enviadme un e-mail y os lo recordaré.

EN HONOR A HAWKING

            "Mis expectativas se redujeron a cero cuando tenia veintiún años. Todo desde entonces ha sido un extra".


        La teoría de la relatividad de Einstein se basa en una premisa muy sencilla. Tan sencilla que a muchos físicos teóricos y experimentales de máximo nivel les parecía imposible: la velocidad de la luz es independiente del observador. O lo que es lo mismo, si intentamos medirla nos encontraremos que siempre vale lo mismo…. aunque estés quieto en la Tierra, parado en la superficie de Marte, subido a la Estación Espacial Internacional o viajando a la misma velocidad de la luz en una nave espacial del futuro.

            Pero el desarrollo matemático de la relatividad (restringida y general) lleva a conclusiones muy complejas como la deformación del espacio, la contracción del tiempo, ver estrellas detrás del Sol que no deberíamos ver o fenómenos todavía mas imposibles de imaginar.

            Hacen faltas mentes muy potentes y profundas para sondear las ecuaciones y transformar números e infinitos en sucesos o fenómenos naturales de cuya existencia o naturaleza no sabemos nada. Un  auténtico reto para los físicos: no es ser capaz de matematizar (reducir a ecuaciones matemáticas) un fenómeno real que existe y estudio; es ser capaz de resolver una ecuación (o una parte de ella) y pensar un fenómeno real (del cual no sospecho a priori siquiera de su posible existencia) que la explique.

            Pocos científicos están a esta altura y uno de ellos es Stephen Hawking (Oxford, 1942).  Y lo consiguió además con una terrible dificultad añadida: con 21 años se empezó a manifestar en su cuerpo una enfermedad degenerativa muy grave  llamada ELA (le llegaron a pronosticar dos años de vida), que lo dejó paralizado en una silla de ruedas a muy temprana edad. Pronto su cerebro quedó confinado en un cuerpo atrofiado con poca esperanza de vida. Lo superó: su mente viajaba por el tiempo y el espacio, allá donde no hay ataduras corporales; soñando con estrellas masivas y luces de otros tiempos, cerca del no lugar donde empezó el Universo, donde comenzó el tiempo, donde nació una promesa de vida que cuajó en un planeta pequeño de una estrella común en un brazo de una galaxia mas común todavía.

            Los estudios sobre relatividad llevaron a  Hawking (junto con Roger Penrose) a postular en 1960 que el Universo tuvo que empezar en un estado de densidad de energía infinita: el big bang del que hablaban algunos físicos como G. Gamow.  Teoría aceptada por los cosmólogos y demostrada experimentalmente  por  Penzias y Wilson al encontrar en 1965 los restos de la gran explosión: el fondo de microondas.

En 1970 Hawking indica la existencia de agujeros negros: zonas del espacio actual donde se dan condiciones parecidas al big bang, lo que se conoce como una singularidad. Los agujeros negros son zonas del espacio donde una masa muy grande (del orden de una decena de masas solares hasta millones, o mas, de masas solares) colapsa sobre si misma, doblando el espacio y encerrando a la materia en una especie de saco que la aísla del espacio normal y lo curva, de manera que la luz no puede salir de él.

Si bien la teoría del big bang se puede “visualizar” a partir del estudio del universo (si el universo se expande, según demostró Hubble, y retrocedemos mentalmente hacia atrás en el tiempo nos damos cuenta de que todo él tuvo que estar concentrado en un espacio muy pequeño o incluso nulo) el concepto de agujero negro es totalmente ajeno a  nuestra experiencia. Hawking tuvo que pensar como interpretar un infinito matemático (la singularidad en el espacio normal) en un objeto real que existe en la naturaleza.

Todos estos estudios y otros le llevaron a obtener  en 1979 la cátedra Lucasiana de Matemáticas de la Universidad de Cambridge, la mas famosa y exclusiva del mundo, compartiendo honores con los físicos mas grandes de la historia como I.  Newton. Y todo ello mientras la enfermedad progresaba y limitaba su vida personal (en 1985 se quedó sin habla y solo se podía comunicar a través de movimientos faciales que controlaba un sintetizador de voz) .

 En años posteriores Hawking amplió su fama entre el mundo fuera del académico, pues a sus logros profesionales,  como el descubrimiento de la radiación Hawking  (radiación emitida por los agujeros negros en su horizonte con el espacio) o sus avances en la necesidad de unificar la teoría cuántica con la relatividad (que hoy llaman teoría del todo);  unió su actividad como divulgador científico en libros como  “Breve historia del tiempo”.

Fama que le ha llevado a obtener numerosos premios, aparecer en series de tv y dar conferencias por todo el mundo. Por ello son muy conocidas sus ideas personales: la humanidad sólo podrá sobrevivir si coloniza el espacio, el hombre no debería a contactar con especies extraterrestres (ya sabemos que le pasó a los indios en Norteamérica), Dios no existe (la ciencia da una explicación suficientemente  convincente de la naturaleza) o las mujeres son el misterio mas total e insondable que se conoce.

Hoy el cuerpo de Hawking colapsó. Pero al igual que sus estrellas colapsan en objetos maravillosos, su mente colapsó hace tiempo en ideas todavía mas singulares y maravillosas. Hoy nos abandona el genio. Sus ideas nunca lo harán.

EL UNIVERSO CAÓTICO

         Sábado por la mañana. Leo en la prensa digital que los partidos políticos se han puesto de acuerdo en que es necesario formar mas y mejor a los profesores. Me cabreo: lo que realmente quieren decir es que han llegado a la conclusión de que el desastre del actual sistema educativo no se debe a ellos (sus diseñadores y hacedores) ni al resto de la sociedad (los votantes nunca pueden ser tachados de responsables de algo) sino que los culpables son los profes, que dejan mucho que desear en su calidad y formación.

         Sábado por la tarde. Leo un libro de ciencia-ficción china (si, lo reconozco: soy un friki que hace esas cosas) y, al leer cierto párrafo, se me ocurre que es perfecto para usarlo como cebo cuando explico a mis alumnos lo que significa el primer principio de la termodinámica.

        ¿Leer ciencia ficción es bueno para la formación de un profesor de física?, ¿leer divulgación científica sobre astronomía o nuevos avances en mecánica cuántica es bueno para mi formación?. Supongo que no lo será para los pedagogos sabelotodo de nuevo cuño y los políticos que los escuchan a ellos y no a nosotros, pobres seres indocumentados, resabiados y antiguos.

       Pero la ciencia es difícil de entender. Es abstracta. La ciencia no se ve, se piensa. Y esto es muy complicado para el alumno en la era tecnológica digital en la que vive inmerso, una era en la que la imagen (instagram, youtube, la tele) lo es todo.

       El cerebro del alumno está diseñado igual que hace 100.000 años. Es un cerebro concebido para detectar y escapar del tigre dientes de sable, localizar bayas comestibles, perseguir megaloceros en densos bosques o cazar mamuts en heladas estepas. No está diseñado para abstraerse y ponerse a pensar en cosas tontas. Por eso es importante que el profesor de ciencia busque como activar el interés por lo que se explica.

       Y eso incluye leer ciencia ficción y contar sus historias en clase o en un post sobre el primer principio de la termodinámica.

      Así que imaginen el siguiente experimento: Coloquemos una bola de billar negra muy cerca de la tronera y una bola blanca muy cerca de la bola negra. Damos un pequeño golpe a la primera y la bola negra entra mansamente en el agujero,

      Repitamos el experimento cinco minutos después y observaremos que si golpeamos a la bola blanca con una  fuerza similar, la bola negra volverá a entrar mansamente en la tronera igual que antes.

     Giremos la mesa de billar noventa grados y repitamos el experimento golpeando a la bola blanca de igual manera que antes. ¿Qué ocurrirá?. Pues que observamos el mismo resultado que las dos veces anteriores.

      Podemos repetir el experimento las veces que queramos, variando posiciones de la mesa (rotándola o moviéndola) y tiempos, pero si golpeamos la bola blanca de la misma forma, el aburrido resultado será: la bola negra entra mansamente en la tronera.

       ¿Qué conclusión sacamos?. ¿No lo adivinan?, ¿No?. Alucinen: las leyes de la física son invariantes (no cambian) en el tiempo y en el espacio.

      Piensen que si esto no fuera así, el resultado de cada experimento podría ser diferente cada vez: una vez la bola negra se podría quedarse parada y otra podría salir disparada a una velocidad cercana a la de la luz. El universo  no sería como es. Sería un universo impredecible, caótico.

       El primer principio de la termodinámica nos dice que las leyes de la física son invariantes con el tiempo, lo que equivale a decir que la energía se conserva. Por eso la velocidad de la bola negra es siempre la misma tras el golpeo de la bola blanca: la energía de la bola blanca se transfiere parcialmente a la negra, pero la suma de la energía antes y después del choque es la misma. El resultado del experimento es el mismo.

      Si la energía no se conserva, la bola negra podría salir con diferente velocidad cada vez. El experimento tiene diferentes resultados en el tiempo.

       ¿Qué ocurriría si el universo no conservara la energía?.  Imaginen  un universo estable como el nuestro, con leyes inmutables y seres que piensen sobre él. Imaginen que, de repente, esos seres observan que la energía no se conserva, que las leyes de la física no son inmutables en el tiempo.

       ¿Pueden imaginarlo?, ¿pueden?. No "se rayen": pidan ayudan a un experto con mas imaginación que nosotros. Lean “El problema de los tres cuerpos” de Cixin Liu. Lean ciencia-ficción china. Sean un friki.

¿QUÉ ES LA LUZ?

     Este es el tercer año consecutivo que doy clase a un grupo de alumnos de los que podríamos calificar de “simpáticos”. Ese tipo de grupo que podría ser académicamente excelente pero que, por no callarse ni debajo de agua, termina siendo un curso “bueno a secas”.  Porque cuando el grupo está más pendiente de hacer gracietas o de cómo dice las cosas el profesor (para “sacarle punta”) y no de lo que está realmente explicando, el resultado académico se resiente inevitablemente. Y más si estas en segundo de bachillerato y te la juegas todo a la carta de la selectividad.

      Pero la desaparición por deserción de los “elementos” mas perturbadores, hace que este año las cosas vayan un poco mejor. Así que hay alumnos, como María, que ya son capaces de hacer preguntas muy interesantes sobre el tema de clase, preguntas que superan el mero conocimiento que se les exigirá. En ese momento es cuando un profesor puede disfrutar de verdad, enganchando a la clase con historias interesantes o con la belleza intrínseca de la ciencia. Entonces, cuando el profe cautiva al alumno, la enseñanza se convierte en arte, tal y como sabiamente intentó explicar una vez el orientador del IES San Isidoro a un grupo de padres  de esos que creen saber enseñar mejor que los propios profesionales.   

    Así que intentaremos disfrutar María y yo ( y espero que también los amables lectores) de cómo se desentrañó la naturaleza de la luz.

    La luz siempre ha sido un gran misterio para el hombre. Durante miles de años muy poco sabíamos sobre ella. El primer hombre en proponer una idea coherente sobre ella fue Isaac Newton en 1666. Para Newton la luz estaba formada por pequeñísimas partículas (corpúsculos), que viajaban extremadamente rápido; tanto que su velocidad no podía ser medida (incluso Galileo, padre de la ciencia, había fracasado en el intento). Con esa idea Newton fue capaz de explicar lo poco que se sabía de la luz: viajaba en línea recta, se reflejaba en una superficie pulida, cambiaba de dirección al pasar del aire al agua o se dispersaba al pasar por un prisma.

   Sin embargo su “teoría corpuscular de la luz” tenía varias grietas, entre ellas, que los rayos de luz podían entrecruzarse sin perturbarse entre ellos. Para evitar este inconveniente Huygens (1678) propuso que la luz era una onda de algún tipo. Esta “teoría ondulatoria de la luz” explicaba casi todo lo conocido sobre ella, excepto su propagación en línea recta y su capacidad para propagarse en el vacío (entre el Sol y la Tierra, por ejemplo), ya que una onda como el sonido necesita un medio para propagarse (aire, agua).

   Durante unos cien años ambas teorías compitieron sin que pareciese haber un claro triunfador, hasta que la situación cambió en 1800. En ese año un científico inglés, Thomas Young, hizo pasar rayos de luz por dos orificios muy pequeños y juntos, recogiendo la luz saliente en una pantalla. El resultado del experimento fue una serie de bandas (franjas) alternas de luz-oscuridad, que sólo podía atribuirse a una naturaleza ondulatoria de la luz. 

   La balanza pareció inclinarse definitivamente hacia la teoría ondulatoria cuando Fresnel propuso una explicación matemática clara de los fenómeno implicados en el experimento de Young (y los suyos propios): la  longitud de onda muy corta de la luz respecto a otras ondas explicaba su extraño comportamiento de viajar en línea recta y lo dificultoso de reproducir fenómenos de difracción e interferencia (las franjas de Young).

   A pesar de esto quedaba pendiente de explicación la capacidad de la luz de propagarse sin un medio aparente. La solución empezó a vislumbrarse en 1860 cuando James Clerck Maxwell presentó a la comunidad científica un conjunto de ecuaciones que unificaba y explicaba los fenómenos eléctricos y magnéticos en una sola fuerza electromagnética.

   Según Maxwell una carga quieta deforma el espacio a su alrededor de una cierta manera que llamamos campo eléctrico. Cuando la carga se mueve se genera, además, otra deformación del espacio que llamamos campo magnético. Pero ambos campos interaccionan entre sí, de manera que un campo eléctrico genera uno magnético a su alrededor y el nuevo campo magnético otro nuevo campo magnético, que genera uno eléctrico y así sucesivamente.

    Esta situación es exactamente igual a lo que ocurre cuando tiramos una piedra en el agua, La piedra “empuja” el agua hacia abajo y el agua empujada “tira” del agua a su alrededor, que tira a su vez del agua a su lado y así sucesivamente hasta que vemos una onda (una ola).

    Por lo tanto, Maxwell proponía que una carga en movimiento generará ondas electromagnéticas en el espacio que la rodea. Estas “ondas electromagnéticas” tendrían propiedades sospechosamente parecidas a las de la luz, incluida su capacidad para propagarse en el vacío.

    ¿Pero es cierto que una onda electromagnética es luz?.  El bingo lo cantó Hertz en 1887 al ser fue capaz de producir ondas electromagnéticas a partir de un circuito eléctrico. Ondas que eran indistinguibles en propiedades de las de la luz. Con esto la batalla había sido ganada definitivamente por la naturaleza ondulatoria de la luz.

      Pero, contra todo pronóstico y para mayor asombro de la comunidad científica, en el mayor triunfo de la teoría ondulatoria estaban las semillas de su mayor fracaso. Los experimentos de Hertz llevaron a otro científico, Lenard, a encontrar que la luz podía arrancar electrones de ciertos metales y producir una corriente eléctrica en un circuito. Este “efecto fotoeléctrico” (por el que recibirá el premio Nobel en 1905) tenía una serie de características que no podían ser explicadas de ninguna manera suponiendo que la luz era una onda.

    Si un cierto metal emitía electrones con luz amarilla, resultaba que en ningún caso podíamos obtener el efecto fotoeléctrico con luz roja (de menor energía), aunque esta fuera muy intensa. Si intensificamos el rayo de luz amarilla conseguiremos que salten un número mayor de electrones (lo esperado), pero todos viajaban a la misma velocidad. Si la luz fuese una onda deberíamos obtener también electrones mas veloces al intensificar la luz amarilla, de la misma manera que esperaríamos ver el efecto fotoeléctrico al aumentar la intensidad de la luz roja.  Además si usamos luz azul (mas energética que la amarilla) veremos electrones mas veloces, pero un aumento de la intensidad conduce a mas electrones igual de veloces, nunca se traduce en electrones mas rápidos.

   Al final fue Albert Einstein el que tuvo que acudir al rescate de la ciencia en 1905.  Su explicación del efecto fotoeléctrico (Premio Nobel de 1922) resucitaba la teoría corpuscular.  La luz, explicaba Einstein, está formada por partículas llamadas fotones, cuya energía dependía de la frecuencia (magnitud de la onda que indica su energía) del haz de luz. Cada átomo individual sólo puede coger un fotón, de manera que la velocidad del electrón que salta depende de  la diferencia entre la energía total que lleva el fotón y la energía necesaria para el salto.

   Los fotones rojos llevan una energía menor que la que necesita el electrón para saltar: el efecto fotoeléctrico nunca ocurre. Los fotones amarillos llevan una energía superior a la precisa para el salto, así que saltan electrones de cierta velocidad. Si intensificamos el rayo amarillo, hay mas átomos que cogen fotones pero todos ellos emiten electrones de la misma velocidad (todos los fotones amarillos son iguales). La luz azul implica fotones mas energéticos, por lo que los electrones que saltan son mas veloces… pero se cumple todo lo que hemos explicado para la luz amarilla.

   Final sorprendente y guerra ganada por la teoría corpuscular de la luz.

 ¿Seguro?. Pues no. Hemos dicho que la energía del fotón depende de la frecuencia del haz.. pero la frecuencia es una magnitud típica de las ondas, no de las partículas. La solución real aportada por Einstein es que la luz tiene una naturaleza dual onda-corpúsculo. A veces se comporta como una onda (difracción, arco iris, bandas de interferencias) y a veces como partículas (imágenes en una pantalla, efecto fotoeléctrico).

   Es como dos caras de una misma moneda. ¿De que depende que salga cara o cruz?. De lo que el observador haga. Exactamente igual que verá usted una cara u otra de la moneda según lo que usted haga.

   ¿Contradictorio?. No, complementario. ¿O es que usted siempre se comporta igual en todas las ocasiones?

¿QUÉ ES DEMOCRACIA?

     Definitivamente el corral está revuelto en nuestro país. Incluso los alumnos de mi centro hablan entre ellos, a veces acaloradamente, sobre la cuestión catalana. En el fondo de esas discusiones gira un concepto: el de democracia. ¿Por qué no aclarar un poco las dudas?.

      La democracia es otra realidad imaginada de la que hablaba en mi último post. Es un concepto abstracto que NO EXISTE en la realidad, por lo que no podemos comparar con la realidad para comprobar lo que ésta es. Comprobar que la gravedad es siempre atractiva es fácil: basta con soltar un objeto en presencia de ella y todos veremos que el objeto cae hacia abajo, por lo que todos estaremos de acuerdo en que la gravedad es atractiva.

       Por el contrario hay o puede haber tantos conceptos de democracia como personas haya. Así que para definir democracia tendremos que ponernos de acuerdo entre varias personas sobre su significado. En definitiva: será democracia lo que un grupo de homo sapiens diga que es democracia. Y puede ocurrir perfectamente que dos grupos de sapiens tengan dos conceptos diferentes de democracia y no se pongan de acuerdo. Esto es lo que ocurre hoy en España.

      Parece ser que para los independentistas catalanes, democracia es votar. Da igual, a lo que se ve, cómo se vota, el qué se vota, quién vota y para qué se vota. Lo importante es votar. ¿Es esto democracia?.

      La democracia nace en la ciudad-estado de Atenas en 500 aC. De las aproximadamente 300.000 personas que vivían en ella, sólo podían votar los varones adultos que tenían la condición de ciudadanos, unos 30.000 (un exiguo 10 %). En Atenas había muchas personas que eran muy importantes para la ciudad (comerciantes por ejemplo) que nacían y morían en la ciudad, pero no eran  ciudadanos y no podían votar, incluidas las mujeres. ¿Diríamos hoy en día que esto era una democracia en términos modernos?. No, pero se votaba.

       Roma antes de ser Imperio era una república. También se votaba. Pero sólo votaban (otra vez) los varones adultos con la ciudadanía romana. Y el sistema estaba amañado, de forma que los aristócratas tenían mucho mas poder decisorio en las votaciones que los que no lo eran. De hecho la mayor parte de los magistrados y los jurados eran elegidos de las élites dominantes: los Julios (Césares), los Bruto, los Cecilio, los Escipiones ocupaban generación tras generación los cargos mas altos. Y al ser ellos mismos jueces y reos, era muy difícil que los juicios fueran ganados por la otra parte. Esto es lo que ocurre cuando no hay separación entre el poder judicial y el legislativo. Hoy diríamos que eso no era democracia… pero se votaba.

     Cuba, año 2017. Un dictador, hermano de otro dictador, dirige con mano de hierro la república cubana. Sólo hay un partido (puedes ser comunista o comunista). Teóricamente cualquiera puede ser elegido, pero si no tienes poder dentro del partido comunista nunca saldrás elegido. Pero se vota.

      Podemos concluir que la democracia no consiste sólo en votar. Hay que exigir mas garantías. Un aspecto fundamental es la legalidad en la que se desarrolle la votación. La legalidad afecta al qué se vota y al cómo se vota.

       Supongamos que en  la comunidad autónoma de Andalucía andamos locos por votar que se quite el derecho de voto a las mujeres o a los homosexuales. Esto es ilegal porque nuestra Constitución dice que no podemos ser discriminados por razón de sexo u orientación sexual. ¿Nos parecería correcto y democrático celebrar un referéndum en Andalucía para lo dicho?. Creo que a nadie nos lo parecería. ¿Por qué entonces hay muchas personas que sí se lo parece si lo que se vota es algo igual de ilegal como es separar Cataluña de España?.

    La respuesta es sencilla: no lo ven igual porque no quieren verlo igual. Puede mas su deseo, su imaginación de una Cataluña lliure, que la fuerza de los argumentos. Están dispuestos a olvidar lo que sea y a hacer lo que sea para conseguir su sueño.

    Porque en democracia también es muy importante la forma en la que se consigue realizar las cosas.  El referendúm se ha celebrado vulnerando las leyes de España, al ir en contra de la constitución; las leyes del estatuto de Cataluña, por la forma en la que se aprobó en el parlamento catalán; la ley del referéndum aprobada por ellos mismos (cambiaron, por ejemplo, la forma de votar minutos antes de empezar). ¿Cómo puede ser democrático una votación en esos términos?. Y Además la forma de celebrarlo: sin censo, sin junta censal, sin urnas ni papeletas oficiales, votando la misma persona varias veces, votando niños, votando sin identificación, votando en la calle, con urnas llenas antes de empezar; en fin sin un recuento fidedigno de votos.

        Este aspecto de legalidad es básico, pues la legalidad es lo que garantiza el derecho de todos. La frontera entre mi derecho y el tuyo es la ley. Si la frontera la marca alguien, ese alguien pondrá sus derechos muy por encima de los míos (el ancho del embudo para mí y el estrecho para ti, es algo muy tentador para un homo sapiens). Nunca sabremos seguro cuales son mis derechos, serán los que ellos, a conveniencia, digan que son.

     Que no se dude: un verdadero demócrata es el que defiende la ley de una democracia, la acata y, si no le gusta, la intenta cambiar mediante pautas legales. Lo contrario acabará, sí o sí, en abuso del más débil.

  En democracia los cambios en la Constitución, deben ser muy bien pensados. Porque la Constitución señala el camino de las normas fundamentales de convivencia ente los miembros de la comunidad. O sea, los españoles. Por eso resulta inquietante esta pregunta: ¿Para qué se quiere separar Cataluña de España?.

      Vivimos desde hace miles de años en un proceso de globalización. Se piensa que la globalización es algo nuevo. Pero no es cierto, ya estaba en la conversión de bandas de cazadores-recolectores en aldeas, éstas en ciudades y las ciudades en imperios. Lo que ocurre es que el proceso se ha acelerado en el último siglo.

     Y ahora que por fin la unión es tal que las guerras salen mas caras que la paz y que Europa y España gozan de un nivel de bienestar nunca vistos, ¿se pretende trazar mas fronteras que nos debilitan, nos dividen y generan menos bienestar?. Y no es un invento, ya Cataluña lo vive con la fuga de empresas y la huida masiva del turismo. ¿Un corralito financiero en la nueva república genera riqueza o la destruye?. ¿Estar fuera de Europa genera riqueza o la destruye?. 

      ¿Para qué entonces?. Todo se hace parar “ser libres”.

     Y volvemos a la idea inicial. Para los independentistas ser “libres” es más importante que ser “demócratas” o tener más “bienestar”. Como democracia, libertad y bienestar son realidades imaginadas, es perfectamente factible hacer las tres compatibles en cualquier mente, subordinando si hace falta las segundas a la primera: basta con ponerse  de acuerdo entre ellos sobre lo que significa ser libres (ser independientes de España), ser demócratas (votar lo que ellos digan que es legal y cómo ellos digan que es legal) y tener bienestar (vivir en una Cataluña libre sea cual sea su realidad económica y social).

LA REALIDAD IMAGINADA

      En la primavera he leído un libro fantástico: “Homo Sapiens” de Yuval Harari. Cuenta la historia de cómo nuestra especie, homo sapiens sapiens, pasó de ser un homínido mas que lucha por sobrevivir a sus depredadores mientras caza y recolecta, a ser literalmente el dueño absoluto del planeta. El cambio que nos permitió tal proeza se llama revolución cognitiva.

      La revolución cognitiva es la capacidad del hombre que le permite pensar en abstracto, imaginar realidades que no existen y transmitirlas entre los individuos para trabajar juntos.

      Estas “realidades imaginadas” permitieron que muchos hombres colaborasen entre ellos para conseguir fines mayores. Una de las realidades imaginadas mas potentes es la religión. El imperio egipcio se aglutinó en torno a la idea de un faraón que era un dios viviente, responsable de la prosperidad del pueblo. La promesa de una vida eterna al final de la muerte llevó a la construcción de inmensas catedrales.

Otra realidad imaginaria muy poderosa es la de nación. No nacemos siendo de una nación. Si así fuese bastaría con una mirada para saber de qué nación somos, igual que basta una mirada para saber si somos hombres o perros. Pero sólo somos españoles si un papel dice que lo somos y el resto de los españoles están de acuerdo con ese papel. Si además todos los que decimos ser españoles trabajamos juntos, podemos conseguir prosperidad o construir grandes infraestructuras que generan mas bienestar. Esta es la promesa de las realidades imaginadas: la obtención para el individuo de algo mucho mejor.

Y lo sorprendente es que pueden funcionar. Todos los españoles colaborando juntos, ayudándonos mutuamente, creando otras poderosas realidades imaginadas como nuestra Constitución o nuestra democracia, hemos conseguido altas cotas de prosperidad.

Pero todas estas realidades, estas culturas, tienen un talón de Aquiles: al existir sólo en nuestro cerebro funcionarán sólo si creemos en ellas, pues no pueden ser contrastadas con la Realidad. Lo que está ocurriendo en nuestro país es una clara muestra de ello. Hay catalanes que quien sustituir en su cabeza la realidad imaginada “España” por la de “Cataluña”. Como no se nace español o catalán, basta con pensar que se es catalán y no español para cambiar una por otra.

Y podemos conseguir el cambio de paradigma negando las veces que haga falta la existencia de cualquier otra realidad imaginada. Así los independentistas no tienen problema alguno en negar las leyes españolas o las suyas propias: laminan los derechos de la mayoría de los catalanes saltándose los procedimientos aprobados por el propio parlamento catalán o cambian una hora antes de empezar el proceso para votar en el referéndum, método que ellos mismos habían aprobado en su propia ley una semana antes. Como el concepto “referéndum” no es algo real, sirve que muchos de ellos estén de acuerdo en decir que el referéndum es válido para que lo sea.

Exactamente igual ocurre con la idea “democracia”. Como solo existe en mi cerebro, será democracia lo que todos digamos que lo es. Si convencemos a suficiente gente de que democracia es votar, dando igual lo que se vaya a votar o cómo se votará, pues entones el 1O será democracia para ese grupo de homo sapiens. Nada de lo que digamos servirá para casi nada: la capacidad de homo sapiens para creer en sus ideas por encima de la realidad es algo innato en nuestros genes.

El que estas culturas solo existan en el cerebro de un homo sapiens explica también la esquizofrenia de tipos como Gerard Piqué. Cuando Piqué salta al Nou Camp con una camiseta con la bandera catalana, en su imaginación lo hace en representación de la idea de “Cataluña”, de un club que es “mes que un club”…. pero cuando juega con la selección española está echando un rato con diez tios mas, con el tonto objetivo de meter mas veces que el contrario una pelota en una portería, mientras 35 millones de homo sapiens imbéciles (en forma de federación española de fútbol ) le pagan dinero por hacerlo. Y a ver quién le demuestra lo contrario.

Pues las imágenes muestran hechos pero no ideas. Si enseñamos dos fotos de Piqué con una camiseta u otra, nunca mostraremos que son dos ideas iguales (dos futbolistas que representan a dos naciones diferentes o dos tios que le pegan patadas a un balón mientras otros homo sapiens pagan por verlo), sólo que se trata de una misma persona vestida diferente.

Exactamente la misma razón de la inexistencia de las ideas justifica que se desee, a veces contra toda lógica, cambiar una realidad imaginada por otra con la promesa de que se estará mejor. Como no es posible demostrar que “España” es mejor que “Cataluña”, basta con imaginarlo para creer que sucederá en la realidad. Como “Europa” existe sólo en la imaginación del homo sapiens, puedo decir que soy Europa o lo seré con total seguridad y sólo me daré cuenta de que no lo soy si los demás europeos me demuestran, a posteriori, y tarde para mi, que no me aceptan como tal.

       Estas promesas son cheques pagaderos en el futuro. Pero un cheque no es un objeto real. No me dan nada real, no puedo contrastar su valor. Pero sí soy capaz de imaginar que Puigdemont pagará ese cheque y veré esa Cataluña de ensueño. Así que colaboro: me echo a la calle, expongo mi cuerpo y el de mi hijo, ejerzo violencia contra los que no piensan como yo. Estoy de acuerdo en que mi violencia es libertad de expresión, la de la policía represión: ¿Acaso no se ve eso en las imágenes de la TV?.

     La solución es difícil para la idea “España”. Los que trabajan por "Cataluña" están unidos, llevan años reescribiendo el pasado a través de la educación y desarrollando ideas imaginarias que los unen, como arrinconar al castellano y aupar la lengua catalana, y no dudan en ejercer violencia (hasta ahora sin daños físicos) contra los otros catalanes que no piensan igual que ellos.

    El bando pro "España" está dividido. En él hay dos partidos claramente constitucionalistas uno de los cuales apoya al gobierno y pide que se active la intervención de la autonomía (el artículo 155). El tercero dice apoyar al Estado mientras pide la reprobación de su vicepresidente (culpando indirectamente de la violencia a sus fuerzas de seguridad), calla ante la violencia independentista contra ese Estado (en forma de jueces, guardia civil, partidos políticos no independentistas o simples ciudadanos catalanes como dueños de hoteles o de empresas no independentistas) y pide diálogo con los mismos que intentan dar un golpe de estado, saltándose por el camino todas las leyes del estado español y las del propio supuesto estado catalán. El cuarto tacha al jefe de estado de antidemócrata mientras acuna antisistemas (y nuestro sistema es una democracia…….), está a favor y en contra de todo y parece mas cerca de los disidentes que del propio Estado.
     
    

UN RAYO DE LUZ

29 de Mayo de 1919. El astrónomo británico Arthur Eddington, con sombrero y gafas circulares, espera ansioso que comience el eclipse. Hace calor y humedad en Isla Príncipe, cerca del ecuador. A su lado varios aparatos enfocan con mucha precisión a trece estrellas cuya posición real ha sido bien establecida por la expedición de la Royal Astronomichal Society  que lidera. Ahora no se ven porque el Sol brilla espléndido en un cielo azul intenso.

Eddington se seca el sudor y escucha como su corazón se acelera: ya se nota como el sol empieza a esconderse tras el disco lunar….

1887. Michelson y Morley miran con perplejidad una vez mas los datos de su complejo y delicado  interferómetro. Los datos insisten machaconamente en  que el querido éter de los físicos  debía volver al limbo de las ideas del que (quizás) nunca debería haber salido. Pero desechar el éter es abrir una ventana a un abismo mental: da vértigo pensar en las consecuencias.

1904. Un joven de veinticinco años sentado en una oficina de patentes piensa en el experimento  MIchelson-Morley. Tiene tiempo para ello: es la ventaja de un aburrido y tranquilo trabajo.  “Aceptemos lo que dicta la realidad. Aceptemos que el esquivo éter simplemente no existe. Aceptemos que la velocidad de la luz es independiente del observador que la mide. ¿Qué significa esto?”. Su mente es poderosa: se propone experimentos mentales con trenes, rayos de luz y tiempo.

Entonces la transformación de Galileo no es válida. No podemos sumar velocidades. Si viajamos a 100 km/h de frente a otro vehículo que se nos acerca a 100 km/h, nosotros mediremos que se acerca a 200 km/h y ésta es la velocidad a la que nos parece chocar. Si el otro coche se aleja a una velocidad de 120 km/h a nosotros nos parece que se aleja(medimos)  una velocidad del coche de 20 km/h.

 Pero si en vez de un coche es un rayo de luz el que se aleja o acerca, mediríamos siempre una misma velocidad 300.000 km/s. ¡ Y esto aunque el rayo de luz se acerque o aleje de nosotros mientras nos movemos nosotros mismos a 300.00 km/s!.

¿Cómo cuadrar las ecuaciones de velocidad para explicar esto?. Solo hay una forma; aceptar una transformación de velocidades que implica que el tiempo pasa de forma diferente según de rápido nos movamos. Si estoy quieto las agujas de mi reloj se mueven rápido. Si me muevo con mayor rapidez mi reloj atrasa. Si soy un rayo de luz el tiempo no pasa, mi reloj está inmóvil. ¡el tiempo es relativo no absoluto!.

Pero si el tiempo cambia la longitud que mido es diferente. ¡El espacio también es relativo!. Las dos cosas, tiempo y espacio tejen una red espacio-tiempo. Son dos aspectos distintos de una misma cosa, una misma realidad.

Demasiado extraño. ¡Pero las ecuaciones son tan bellas, explican de forma tan sencilla los experimentos!.

Marzo de 2017. Llevo tanto  tiempo resolviendo problemas de cinemática que los resuelvo casi por intuición. Eso me lleva a atascarme. El eterno problema del éter que persigue a físicos viejos con poca cintura mental. Ángela me desatasca y les digo a mis alumnos que los profesores que no aprenden algo de sus alumnos (sólo de vez en cuando, sin exagerar) no son buenos profesores.

La otra Ángela de la clase me dice correcto y Rizo se anima y me dice que algún día se alcanzará la velocidad de la luz.

-Imposible- le contesto.

- Que sí- Insiste.

- La velocidad de la luz es un límite inalcanzable- digo yo.

- Pues yo lo he visto en youtube…..

1905. Einstein publica un artículo en Annalen der Physyk en el que expone la teoría especial de la relatividad. En ella demuestra que sólo los fotones de la luz pueden viajar a la velocidad de la luz. Hace falta una masa infinita para que un objeto con masa viaje a la velocidad de la luz.

-          Lo ves, Rizo. Si no tienes masa infinita no pues ir tan rápido.

-          Pues estoy seguro de que aún así se alcanzara algún día- responde.

-          Hombre si Einstein y toda la ciencia del siglo XXI están equivocadas….

1915. Einstein amplía su teoría: es la teoría general de la relatividad. El espacio se curva alrededor de una estrella. Si imaginamos el espacio de tres dimensiones como una lámina flexible y posamos una bola de acero sobre ella, la lámina (el espacio) se curva a su alrededor. Otra pequeña bolita que ruede por la lámina se cae cuando llega a la lámina curvada.

Por lo tanto toda la materia, incluida la luz, viaja (cae) por un espacio curvado (la lámina) cerca de una estrella (la bola de acero). La gravedad no es una fuerza, es una deformación del espacio (y del tiempo) alrededor de un cuerpo masivo.

1919. En el ecuador el eclipse de sol es ya total. Las trece estrellas a las que apuntan los aparatos de Eddington no deberían verse: están detrás del Sol. Eddington mira por el objetivo de las cámaras con el corazón a todo galope y ¡ve las trece estrellas!. ¡Increíble!.

Contra toda lógica la naturaleza se pliega a la mente brillante del joven Einstein y demuestra en todo su esplendor su amor por las matemáticas, por las ecuaciones simples y bellas.

                Un año después Eddington, Dyson y Davidson publican los resultados conjuntos de las dos expediciones (Isla Principe y Sobral, en Brasil) que confirman la curvatura de la luz alrededor del Sol. Fenómeno que permite observar las estrellas detrás del Sol gracias a los 1’74 segundos de arco en la que la luz se curva. Exactamente el valor predicho por Einstein en 1915.

                - Y así- explico a mis alumnos- es difícil pensar que Rizo y youtube puedan tener razón. Una teoría que predice algo tan extraordinariamente ajeno a nuestra experiencia cotidiana como ver algo detrás del sol y que resulta ser comprobado y que además explica tantas otras cosas, incluida la dinámica de Newton, no puede contradecirse tan drásticamente; pues hablamos del núcleo central de la misma: sólo la luz viaja a la velocidad de la luz.

                Rizo levanta la mano pero no le dejo hablar.

                -A menos claro que otro Einstein proponga una teoría mas amplia que, manteniendo la inviolabilidad del límite de la velocidad de la luz en el “universo normal” donde reina la Relatividad, permita burlarlo allá dónde hoy falla la teoría de Einstein. Por ejemplo en el interior de un agujero negro …. o en los hipotéticos agujeros de gusano.